Une première formule mathématique qui peut en dérouter plus d’un, mais qui se révèle exacte…
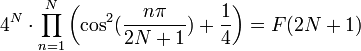
F(N) étant tout simplement le énième nombre de Fibonacci – cf. Bestiaire de formules ou pour les courageux, lire la preuve mathématique.
Les 10 premières itérations de la formule exécutée sous Linux par bc (Basic Calculator) avec ce programme téléchargeable fournissent les résultats suivants:
| N | 2N+1 | F(2N+1) | Résultats de la formule |
| 1 | 3 | 2 | 2.00000000000000000000 |
| 2 | 5 | 5 | 4.99999999999999999968 |
| 3 | 7 | 13 | 12.99999999999999999936 |
| 4 | 9 | 34 | 33.99999999999999999744 |
| 5 | 11 | 89 | 88.99999999999999998976 |
| 6 | 13 | 233 | 232.99999999999999995904 |
| 7 | 15 | 610 | 609.99999999999999983616 |
| 8 | 17 | 1597 | 1596.99999999999999934464 |
| 9 | 19 | 4181 | 4180.99999999999999737856 |
| 10 | 21 | 10946 | 10945.99999999999998951424 |
Une seconde formule…
qui prend ses valeurs parmi les nombres entiers qui sont le nombre de façons différentes de paver un rectangle 2N x 2P par un domino 2 x 1.
Important!
Nous pouvons voir que la première formuleest un cas particulier de la seconde avec P égal à 1.
En marge de la beauté de ces formules, celles-ci peuvent être utilisées pour « tester », « qualifier » et même « valider » des algorithmes de calculs avec des nombres flottants.
